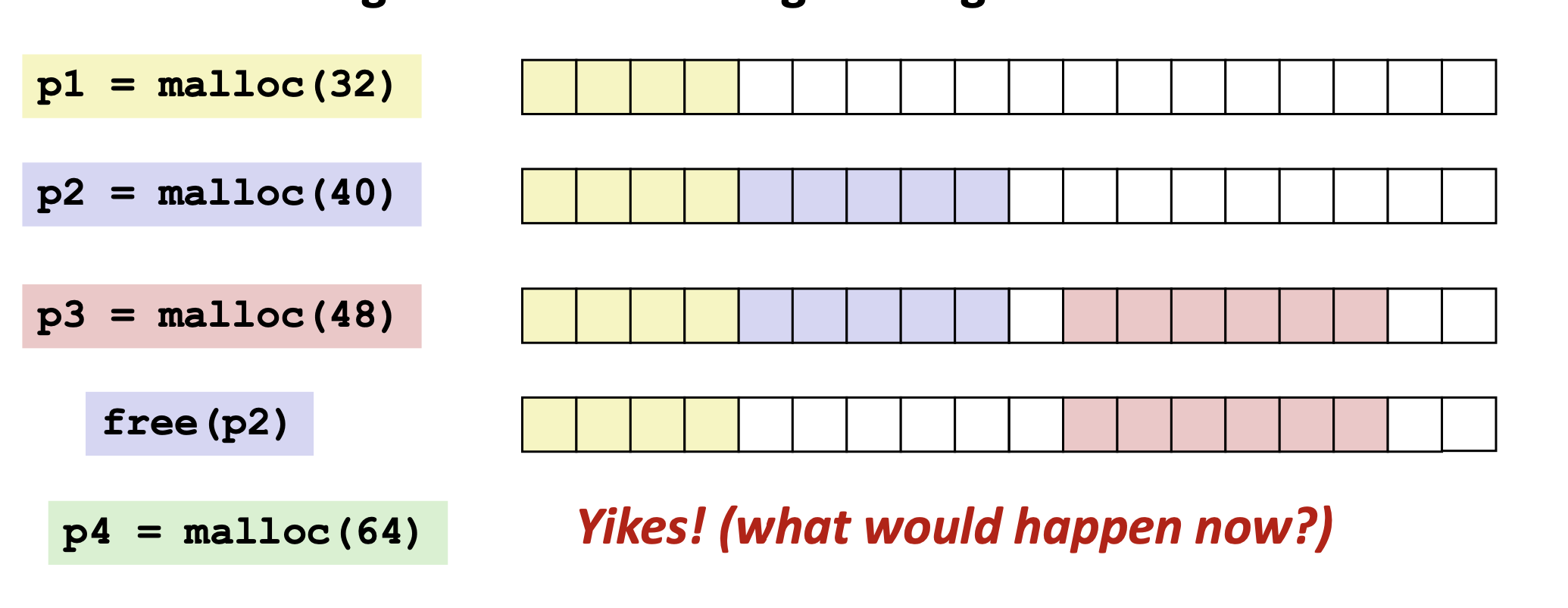
Malloc Simulator

Fragmentation

• External Fragmentation: This occurs when there is enough accumulated space but no single block can fit what is needed.
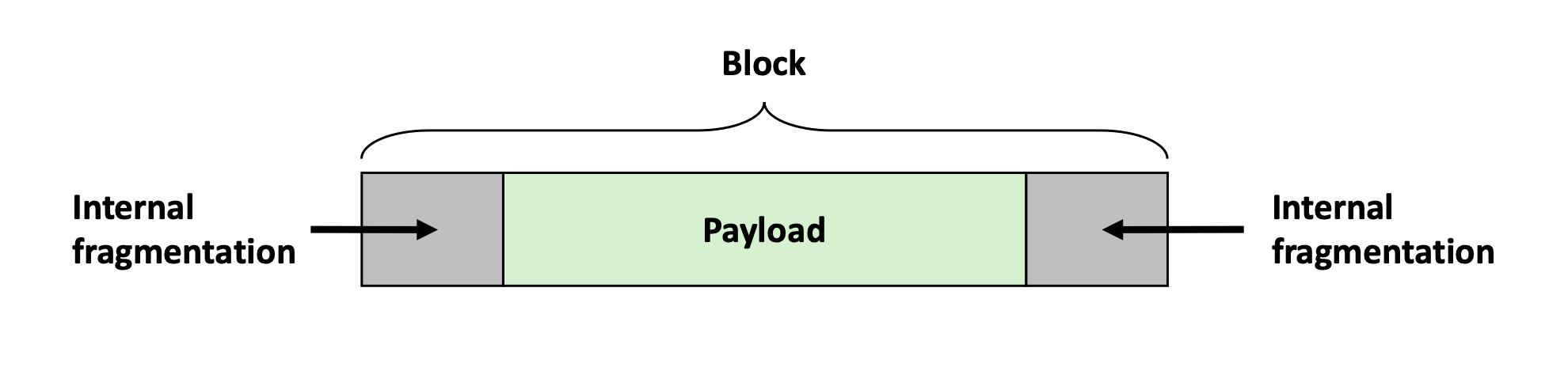
• Internal Fragmentation: Occurs when the actual allocated size exceeds what's needed. For example, headers might take 8 bytes other than the needed space.

how to keep track of free block

• Implicit list
• Explicit list
• segregated list

Splitting policy: When to split

Coalescing Policy: When to Coalesce

• immediate coalescing: coalesce each time free is called
• Deferred coalescing: improve the performance of free by deferring coalescing until needed. Questions need to be addressed: When should I coalesce? If I don't coalesce immediately, how should I get the correct empty space size?

Structure of block

We need the header, next pointer, prev pointers, and payload. For the footer, we don't need to care about it, we just append it at the end of the block.

struct block {
    /** @brief Header contains size + allocation flag */
    word_t header;
    uint8_t payload[0];
};

payload[0]

Footer

What does the footer do?
It indicate whether the current block is allocated or not. After we know this, we can decide if we want to coalesce with the previous block. Also, it contains the size of the blocks, so that we can reach the previous block by minus the size of the previous block and its footer from current block address.

Why do we need footer, isn't that the header already has bit to indicate the current block is allocated?
So that we are able to know if the previous block is allocated or not by checking the previous footer using it's address. When we want to get the address of the previous block, we need the size of the previous block to reach the header of the previous block. The previous footer address can be found using the current block header address minus 8 bytes. Similarly, we can also find the address of the next block and know if it is allocated by looking at its header.

Implicit list

placement policy:

• First-fit: Search list from the beginning, and choose a first free block that fits
• Next-fit: Search list starting where the previous search finished
  Use case: usage would be best if the request space is increasing.
• Best-fit: Search the list, choose the best free block: fits, with the fewest bytes left over

Explicit List

Similar to implicit but need to build a linked list for the free node. One thing need to notice is that now we also need to reserve space in the empty block for the pointer.

struct block {
    /** @brief Header contains size + allocation flag */
    word_t header;
    union {
        uint8_t payload[0];
        struct {
            block_t *prev;
            block_t *next;
        } free_list_pointer;
    } payload_union;
};

We allocated space for prev and next pointer, so now we

/**
 * @brief Insert node into the free list using LIFO
 *
 * @param[in] block A block in the heap
 * @return root of the free list
 * @pre The block is valid
 */
static void free_list_insert(block_t *block) {
    // make sure block != NULL
    // make sure block does not get allocated
    block_t *next = free_list_root;
    block->free_list_pointer.prev = NULL;
    block->free_list_pointer.next = NULL;
    if (next == NULL) {
        // when free_list is empty
        block->free_list_pointer.next = NULL;
    } else {
        block->free_list_pointer.next = next;
        next->free_list_pointer.prev = block;
    }
    free_list_root = block;
}

/**
 * @brief Remove node from the free list
 *
 * @param[in] block A block in the heap
 * @return root of the free list
 * @pre The block is valid
 */
static void free_list_remove(block_t *block) {
    // make sure block != NULL
    // make sure block does not get allocated
    block_t *prev = block->free_list_pointer.prev;
    block_t *next = block->free_list_pointer.next;
    if (prev == NULL && next == NULL) {
        // when it is the only one in free list
        free_list_root = NULL;
    } else if (prev == NULL) {
        // when it is the first
        free_list_root = next;
        next->free_list_pointer.prev = NULL;
    } else {
        // when it is the last
        ...

    }

}

Segregated Free List

Best-fit allows us to minimize fragmentation. But the time complexity is extremely high. So if we combine it with the idea of explicit-list, there is a wonderful idea: what if we use free lists of different sizes? If most of the required space are 25 or 85, why don't we build a free list for those between 24 to 32 bytes? Why don't we build a free list for those between 80 to 88 bytes? Now we have two free list buckets.

So now, we are also able to approximate best-fit in O(k) where k is the number of free list buckets.

Additional Improvement

Eliminate footer

The footer is used to easily look up if the previous block is allocated, and contains size for us to reach the previous block.

But when do we really need to reach the previous block? When coalescing with the previous block.
When do we need to coalescing with the previous block? When the previous block is free.
In conclusion, we only need the previous block's footer when it is free. The same applies for the current block and all other blocks. So we know the block only needs footer when it is free. But we don't need it when it is not.

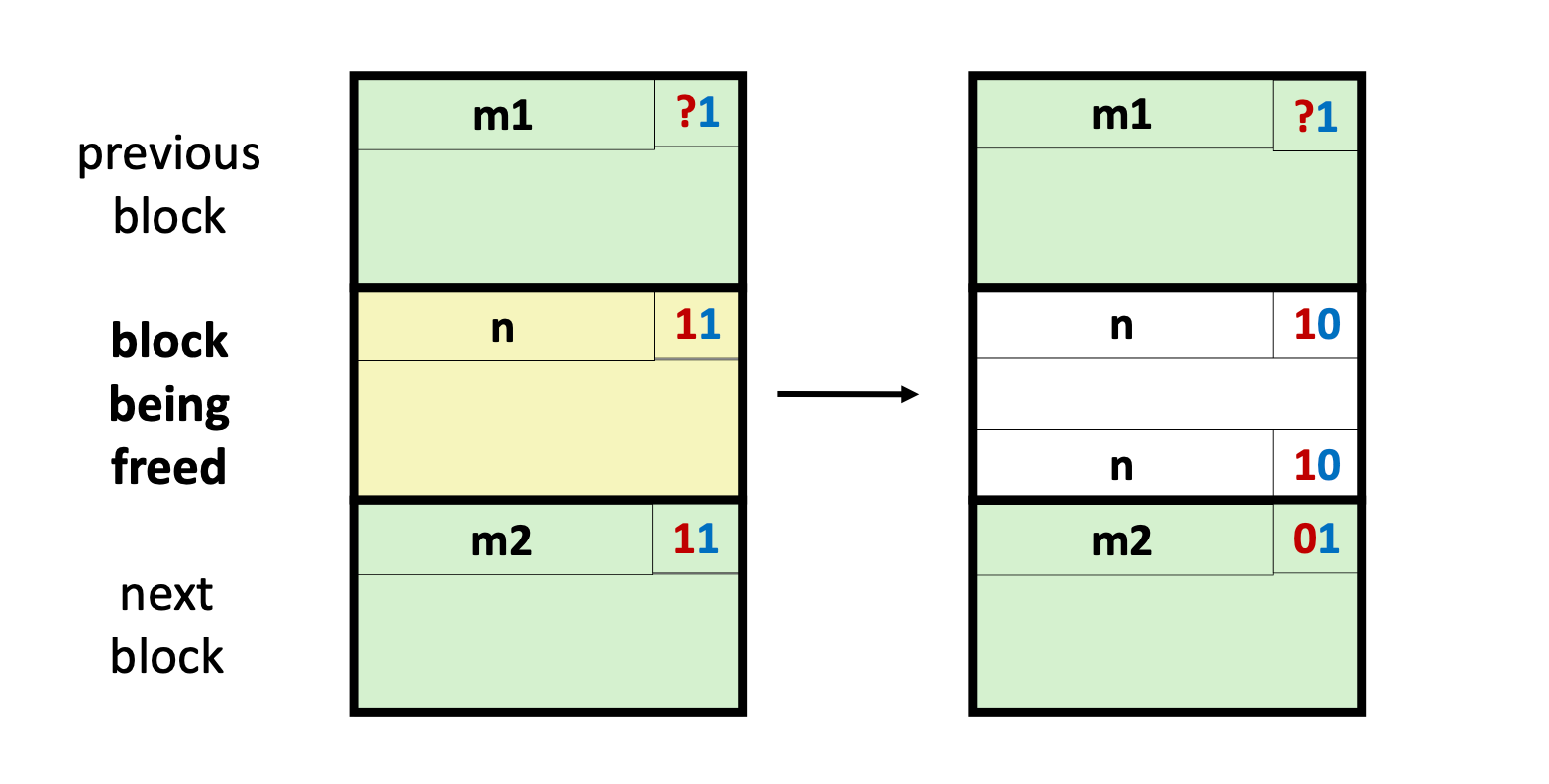
Since our block should be a multiple of 16 bytes and has a minimal size of 32, we can safely assure that there will be space for the footer in the empty spot.

How to reduce the minimal size?

The standard explicit list node would be 32 bytes, 8 bytes for header, 16 bytes for the next pointer and prev pointers. But can we minimize it to 16 bytes? What if we trade time complexity with internal fragmentation?

We can create a free list for mini-block only, as such we are able to ignore the prev pointer. "But our struct still contains the prev pointer, would the space is taken when we malloc?" No, that space will never be used unless we try to access it. So, we should put the prev pointer at the end of the struct.

struct block {
    /** @brief Header contains size + allocation flag */
    word_t header;
    union {
        uint8_t payload[0];
        struct {
            block_t *next;
            block_t *prev;
        } free_list_pointer;
    } payload_union;
};

In this way, this will also work fine for all other sizes of block. For mini-block, we just NEVER access the prev pointer.

Without the prev pointer, how can we find the prev block when we are doing removal of the block? (Insertion does not need prev info since we are attaching node to the tail) Since there is a designated free list for mini-block, there won't be so many free mini-blocks there, so we can traverse the whole free list to find the prev we want.

    block_t *curr = free_lists_head[0].head;
    # requires curr != NULL
    block_t *prev = curr;
    while ((size_t)curr != (size_t)block) {
        prev = curr;
        dbg_requires(curr->payload_union.free_list_pointer.next != NULL);
        curr = curr->payload_union.free_list_pointer.next;
    }

Free List insertion/removal policy

• FIFO
  Have better fragmentation than LIFO because the earlier free block is more likely to have lower address number and keep using up lower address first can fill up the lower address. Else, we keep assigning space everywhere which cause lots of fragmentation instead of filling out one space first.
• LIFO
• Address-ordered policy(increasing)
  Fragmentation is lower but require search every insertion. Fragmentation is lower when applying first fit approach. In this case, we also prioritize need to fill out the space with lower address as described in FIFO.